전기(산업)기사필기/회로이론
자기인덕턴스,상호인덕턴스, 인덕턴스의 결합
손으로 쓰는 성경
2023. 9. 3. 21:12
반응형
●회로이론 18강:자기인덕턴스,상호인덕턴스, 인덕턴스의 결합
●자기인덕턴스 L[H]

\[ L\cdot I=N\cdot\phi \]
| L | 변환상수 |
| I | 전류 |
| N | 코일 감은 수 |
| \[\phi \] | 파이라고 읽고 자속 |
\[e_{L}=N\frac{d\phi}{dt}\]
\[e_{L}=L\frac{di}{dt}[V]\]
\[W=\frac{1}{2}LI^{2}[J]\]
\[W=\frac{1}{2}CV^{2}[J]\]
●상호 인덕턴스 M[H]

\[V_{1}=N_{1}\frac{d\phi}{dt}\,\,\,\,\,\,V_{2}=N_{2}\frac{d\phi}{dt}\]
\[V_{1}=L\frac{di}{dt}\,\,\,\,\,\,\,\,\,V_{2}=M\frac{di}{dt}\]
\[e_{m}=M\frac{di}{dt}\]
\[M=\frac{N_{1}}{N_{2}}L_{2}\]
\[M=\frac{N_{2}}{N_{1}}L_{1}\]
L= 자기 인덕턴스
M=상호 인덕턴스
●결합계수K
\[(0\leq K\leq 1)\]
\[M=K\sqrt{L_{1}L_{2}}\,\,[H]\]
\[K=\frac{M}{\sqrt{L_{1}L_{2}}}\,\,\,(0\leq K\leq 1)\]
●인덕턴스의 결합
*직렬에서 인덕턴스의 결합

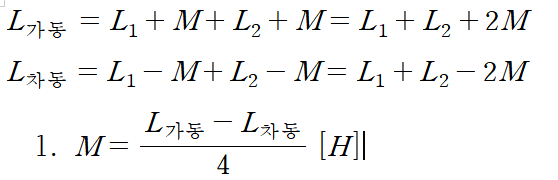
*가동은 전류가 들어가는 방향과 나오는 방향이 서로 같을 때 /자속의 방향이 서로 같을 때
*차동은 전류가 들어가는 방향과 나오는 방향이 서로 다를 때 /자속의 방향이 서로 다를때
*가동 /차동의 기호
점은 들어가는 방향을 의미한다.
| 가동 |  |
| 차동 |  |
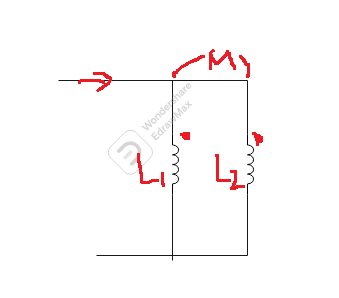
*병렬에서 인덕턴스의 결합
*가동
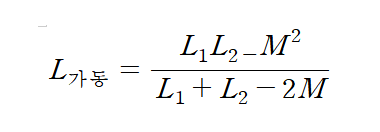
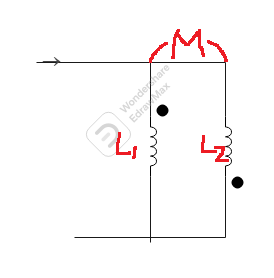
*차동
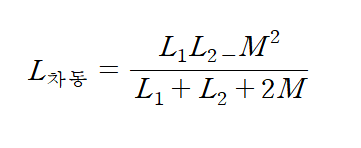
728x90