벡터와스칼라,성분벡터(기본벡터),단위벡터,직교좌표,직각좌표,원통좌표,구형좌표,전기자기학(전기기사)

●전기자기학 1장:벡터와 스칼라

●스칼라:크기만 존재하는 것

●벡터:크기와 방향이 존재하는 것

●벡터 표시법:$\vec{F}$(위에 화살표),  $\dot{F}$(위에 점),  F(진하게 굴게)

$\vec{A}=A\angle\theta$

※A는 크기 $\theta$는 각도(방향)을 나타낸다.

*a+jb

=크기$\times$방향

ex)$\vec{Z}$=3+4j

=$\sqrt{3^2+4^2}\,\,\,\angle tan^{-1}\frac{4}{3}$

 

●벡터의 종류

성분벡터(기본벡터)

단위벡터

직교좌표

직각좌표

원통좌표

구형좌표

 

●성분벡터(기본벡터)

 

 

ex)$\vec{Z}$=3+4j

$\vec{A}=A_{xi}+A_{yi}+A_{zk}$

 

 

●단위벡터...전체의 크기가 1이다.

 

*i,j,k는 성분벡터로 각 각의 크기가 있다.

*벡터=크기×방향

=크기 × 단위벡터

*단위벡터$=\frac{벡터}{크기}$

 

*$\vec{A}=3i+4j$

$=\sqrt{3^2+4^2}=5$

*여기서 3은$A_x$, 4는 $A_y$이다.

 

*단위벡터$=\frac{벡터}{크기}$

$=\frac{3i+4j}{5}$

 

*벡터=크기$\times$단위벡터

$=5\times(\frac{3i}{5}+\frac{4}{5}j)$

=3i+4j

 

*$\vec{A}=3i+4j+5k$

크기$=\sqrt{3^2+4^2+5^2}$

$=\sqrt{50}=5\sqrt{2}$

 

단위벡터$=\frac{벡터}{크기}=\frac{3i+4j+5k}{5\sqrt2}$

 

●직교좌표계:직각으로 교차한다.

 

●직각좌표계

 

 

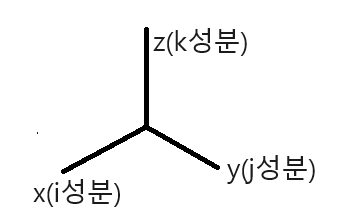
●원통좌표계

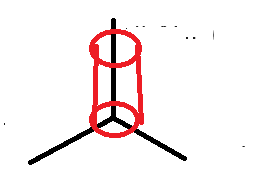
*성분을 r(반지름), $\theta$(각도),Z(높이)로 나타낸다.

 

●구형좌표계

*성분을 r(반지름), $\phi$(파이), $\,\,\,\theta$(각도)로 나타낸다.

 

*ex) $\vec{A}=4i+4j+2k$

크기$=\sqrt{4^2+4^2+2^2}$

$=\sqrt{36}=6$

 

단위벡터$=\frac{벡터}{크기}$

 

$=\frac{4i+4j+2k}{6}$

 

$=\frac{4}{6}i+\frac{4}{6}j+\frac{2}{6}$

 

$=\frac{2}{3}i+\frac{2}{3}j+\frac{1}{3}k$