●회로이론 7강: 순시값, 극형식법, 삼각함수법, 복소수법, 지수함수법
●순시값
*스칼라:크기
*벡터:크기+방향
*순시값
\[ V=V_{m}sin(\omega t+\theta)\]
\[=\sqrt{2}\cdot Vsin(\omega t+\theta)\]
| V | 실효값 |
| \[\theta \] | 위상.쎄타라고 읽는다 |
| \[\sqrt{2}V=V_{m}\] | 최대값 |
| sin | 파형 |
| \[\omega \] | 오메가라고 읽는다 |
| f | 주파수 |
| \[\omega=2\pi f\] | |
| t | 시간 |
*삼각함수
-1은 아크라고 읽는다. 예로 아크 싸인,아크코싸인,아크탄젠트가 된다.

\[sin\theta=\frac{b}{c}\;\:\:\;\:\:\theta=sin^{-1}\frac{b}{c}\]
\[cos\theta=\frac{a}{c}\;\:\:\;\:\:\theta=cos^{-1}\frac{a}{c}\]
\[tan\theta=\frac{b}{a}\;\:\:\;\:\:\theta=tan^{-1}\frac{b}{a}\]
*복소수(j 원래는 i인데 전기 분야에서는 j로 사용한다.)
\[ j=\sqrt{-1}=1\angle 90^{\circ}\]
\[ j^{2}=-1=1\angle 180^{\circ}\]
\[ j^{3}=-\sqrt{-1}=1\angle 270^{\circ}\]
\[ j^{4}=1=1\angle 360^{\circ}(0^{\circ})\]
*벡터
\[\dot{A}=a+jb\]
a:실수부 b:허수부
\[\dot{A}=\sqrt{a^{2}+b^{2}}\;\:\:\:\:\:\:\angle tan^{-1}\frac{b}{a}\]
| \[\sqrt{a^{2}+b^{2}}\] | 크기 |
| \[\angle tan^{-1}\frac{b}{a}\] | 각 |
*순시값
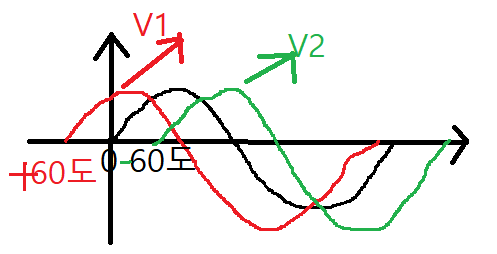
\[ V_{1}=V_{m}\,sin(\omega t+60^{\circ})\]
\[=\sqrt{2}\,V\,sin(\omega t+60^{\circ})\]
\[ V_{2}=V_{m}\,sin(\omega t-60^{\circ})\]
\[=\sqrt{2}\,V\,sin(\omega t-60^{\circ})\]
※V는 실효값
●극형식법:실효값의 크기와 위상으로 표시한 것
\[V_{1}=\,\,V\,\,\angle 60^{\circ}\]
\[V_{2}=\,\,V\,\,\angle-60^{\circ}\]
●삼각함수법
\[V_{1}=V(cos60^{\circ}+j\,sin60^{\circ})\]
\[V_{2}=V(cos60^{\circ}-j\,sin60^{\circ})\]
●복소수법
\[ V_{1}=\frac{1}{2}V+j\frac{\sqrt{3}}{2}\]
\[ V_{2}=\frac{1}{2}V-j\frac{\sqrt{3}}{2}\]
●지수함수법
\[V_{1}=V\,e^{j60^{\circ}}\]
\[V_{2}=V\,e^{-j60^{\circ}}\]
\[e^{j\theta}=1\times(cos\theta+j\,sin\theta)\]
●극형식법의 곱셈 나눗셈
\[\dot{A}=\,A\,\,\angle\theta _{1}\]
\[\dot{B}=\,B\,\,\angle\theta _{2}\]
| 곱셈 | \[A\times B\,\,\angle\theta _{1}+\theta _{2}\] |
| 나눗셈 | \[\frac{A}{B}\,\,\angle\theta _{1}-\theta _{2}\] |
*극형식법의 덧셈,뺄셈:복소수로 변환하여 계산한다. 실수부끼리 더하고 빼고, 허수부
끼리 더하고 뺀다.
\[\dot{A}=10\angle 30^{\circ}\]
\[=10(cos30^{\circ}+j\cdot sin30^{\circ})\]
\[=5\sqrt{3}+j5\]
\[\dot{B}=4\angle 60^{\circ}\]
\[=4(cos60^{\circ}+j\cdot sin60^{\circ})\]
\[=2+j2\sqrt{3}\]
'전기(산업)기사필기 > 회로이론' 카테고리의 다른 글
| R-L직렬회로, R-C직렬회로, R-L-C직렬회로/회로이론 (0) | 2023.08.23 |
|---|---|
| R만의 회로, L만의 회로, C만의 회로. (0) | 2023.08.20 |
| 순시값 평균값 실효값 /회로이론 (7) | 2023.08.06 |
| 직류 교류 주기 위상 (2) | 2023.08.06 |
| 직렬,병렬,배율기,분류기,휘스톤브릿지 (10) | 2023.08.03 |



