반응형
●회로이론 11강:R-L직렬회로, R-C직렬회로, R-L-C직렬회로
*직류에서
교류에서
*z=임피던스, 저항의 총합
Z=R+jX
*X는 리액턴스
●R-L직렬회로

*KCL → 전류 동일, 전류 기준
KVL →

※코사인쎄타를 역률이라고한다. 역률이란 전체에 대해서 실제적으로 한 일에 대한 비율을 말한다.
※쎄타 값은 전압과 전류의 위상차이다.
※Z(임피던스)는 저항의 총합이다.
●R-C직렬회로


역률
●R-L-C직렬회로
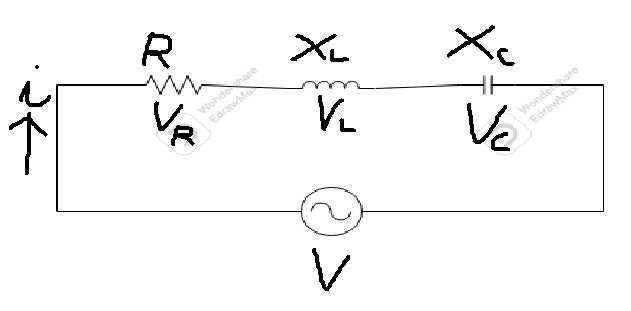
*전류를 기준으로
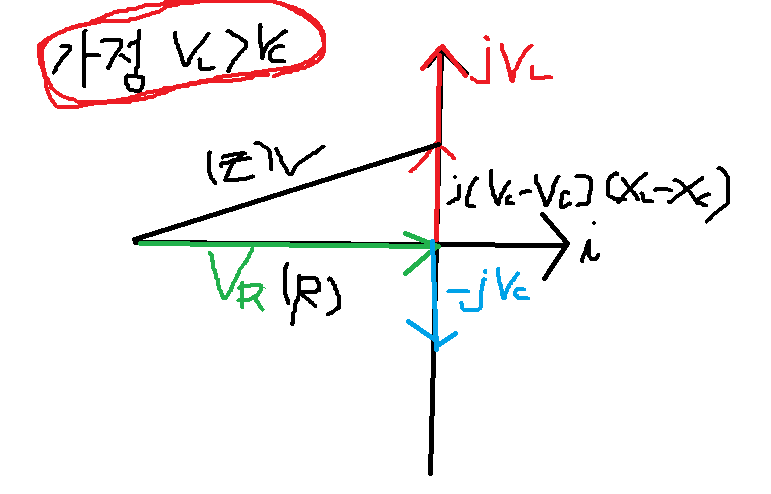
| 유도성회로 | |
| 용량성회로 | |
| 역률 |
728x90
반응형
'전기(산업)기사필기 > 회로이론' 카테고리의 다른 글
| 유효전력,무효전력,피상전력,최대전력전송,복소전력,3전압계법,3전류계법 (0) | 2023.08.29 |
|---|---|
| R-L병렬회로, R-C병렬회로, R-L-C병렬회로, 공진회로 (0) | 2023.08.24 |
| R만의 회로, L만의 회로, C만의 회로. (0) | 2023.08.20 |
| 순시값 극형식법 삼각함수법 복소수법 지수함수법 (1) | 2023.08.07 |
| 순시값 평균값 실효값 /회로이론 (7) | 2023.08.06 |



