※
●회로이론 10장 : R만의 회로, L만의 회로, C만의 회로
수동소자:어떤 전압이나 전류가 있어야만 작동하는 것을 말한다(R.L.C)
| 저항 | 코일(인덕트) | 콘덴서(커패시터) | |
| 기호 | |||
| 단위 | \[ R[\Omega]\] | L[H] | C[F] |
| 읽기 | 옴 | 헨리 | 패럿 |
| 레지스턴스 | 인덕턴스 | 커패시턴스 | |
| 전류가 흐르면 열이나 빛의 형태로 소모하며 전류의 흐름을 방해한다 | 코일에 전류가 흐르면 자속이 발생하고 자속의 형태로 에너지를 저장하며 전류의 흐름을 방해한다 | 전하의 형태로 에너지를 저장하며 전류의 흐름을 방해한다. | |
| \[ G=\frac{1}{R]}[\mho]\] G=컨덕턴스 단위는 모오라고 읽는다. |
\[\omega L[\Omega]\] 오메가엘[옴] w(오메가)는 각속도이고 \[\omega=2\pi f\] \[\omega L=2\pi fl[\Omega]\] |
\[\frac{1}{\omega C}[\Omega]\] 오메가 씨 분의 일[옴] \[\frac{1}{2\pi fc}[\Omega]\] |
|
| \[ X_{L}\] 유도성 리액턴스 |
\[X_{C}\] 용량성 리액턴스 |
||
| x= 리액턴스 | |||
| Z(임피던스) \[Z=R+jX\] \[=R+j(X_{L}-X_{C})\] \[=R+jX_{L}-jX_{C}\] |
|||
*단위를 통일시켜야 계산이 가능해진다.
*컨덕턴스는 저항의 역수이고 병렬 저항 계산할 때 좋다.
*R은 직렬 저항 계산할 때에 좋다.
●저항

W(전력량)=V I t [J]
\[=I^{2}Rt[J]\]
\[=\frac{V^{2}}{R}t[J]\]
●코일
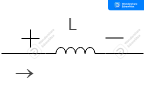
\[\phi=L i\]
\[V_{L}=\frac{d\phi}{dt}=L\cdot\frac{di}{dt}\]
\[W=\frac{1}{2}LI^{2}[J]\]
●콘덴서
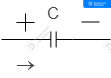
\[Q=C\cdot V\]
\[i=\frac{dq}{dt}=C\cdot\frac{dv}{dt}\]
\[W=\frac{1}{2}CV^{2}[J]\]
●R만의 회로(전압과 전류의 위상이 동일하다)

\[i(t)=I_{m}Sin\omega t\:\:\:\to\:\:\:I\angle 0^{\circ}\]
\[V_{R}=i(t)\cdot R \]
\[=I_{m}R\:\:Sin\omega t \]
\[=V_{m}Sin\omega t\:\:\:\to V\:\angle 0^{\circ}\]
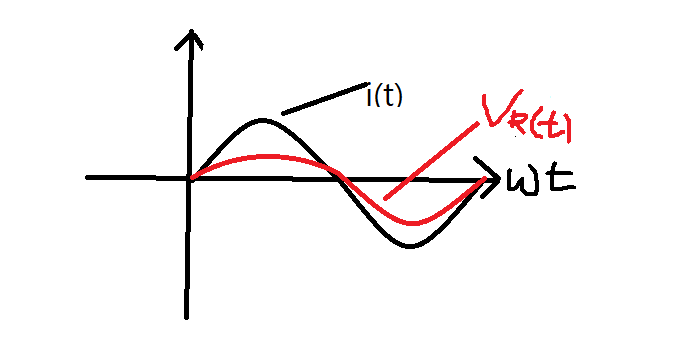
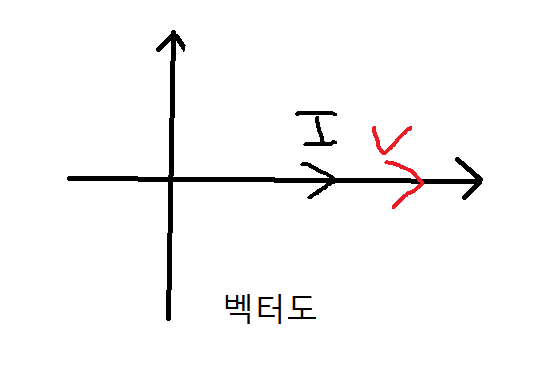
※전압과 전류의 위상이 동일하다.
●L만의 회로(전류의 위상이 전압의 위상보다 990도 느리다)
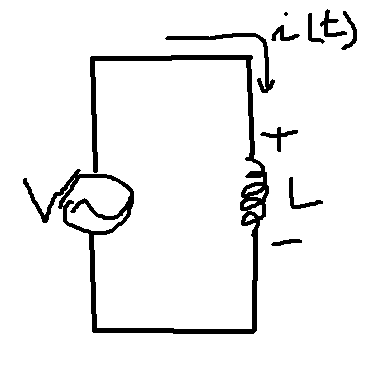
\[i(t)=I_{m}sin\omega t\,\,\,\to\,\,\,I\angle 0^{\circ}\]
\[ V_{L}=L\cdot\frac{di}{dt}=\omega LI_{m}cos\omega t\]
\[=V_{m}Sin(\omega t+90^{\circ})\]\[\,\,\,\to\,\,\,V\angle 90^{\circ}\]
*cos에서 sin으로 변환될 때 +90도가 된다.
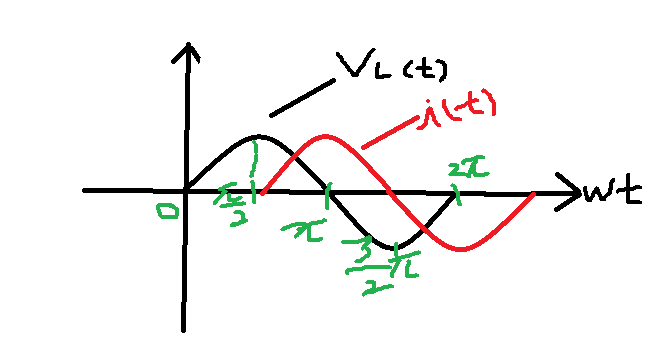
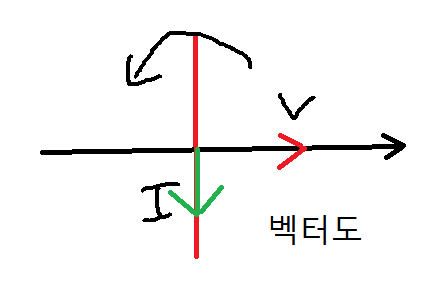
※전류의 위상이 전압의 위상보다 90도 느리다(뒤쳐진다)
\[90^{\circ}=\frac{\pi}{2}\]
●C만의 회로(전류의 위상이 전압의 위상보다 90도 빠르다)
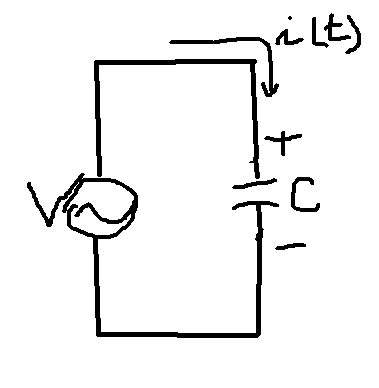
\[i(t)=I_{m}sin\omega t\,\,\,\,\to\,\,\,\angle 0^{\circ}\]
\[i(t)=C\cdot\frac{dv}{dt}\,\,\,=\frac{1}{\omega c}I_{m}Sin(\omega t-90^{\circ})\]
\[=V_{m}Sin(\omega t-90^{\circ})\,\,\,\to\,\,\,V\angle-90^{\circ}\]
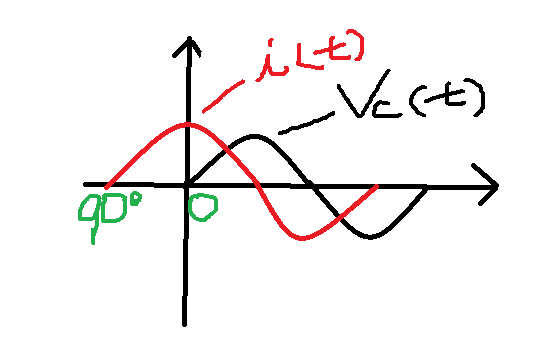
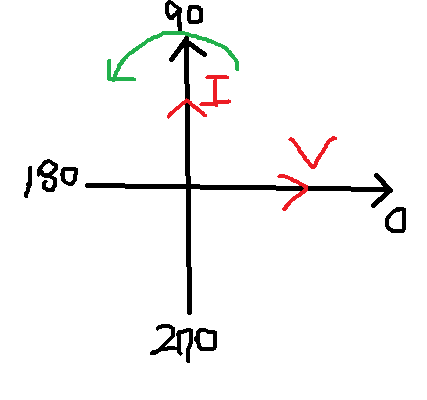
※전류의 위상이 전압의 위상보다 90도 빠르다.
\[90^{\circ}=\frac{\pi}{2}\]
'전기(산업)기사필기 > 회로이론' 카테고리의 다른 글
| R-L병렬회로, R-C병렬회로, R-L-C병렬회로, 공진회로 (0) | 2023.08.24 |
|---|---|
| R-L직렬회로, R-C직렬회로, R-L-C직렬회로/회로이론 (0) | 2023.08.23 |
| 순시값 극형식법 삼각함수법 복소수법 지수함수법 (1) | 2023.08.07 |
| 순시값 평균값 실효값 /회로이론 (7) | 2023.08.06 |
| 직류 교류 주기 위상 (2) | 2023.08.06 |