전원,중첩의 정리,테브난 정리,노튼의 정리,밀만의 정리/회로이론21강

ㅊ회로이론 21강:전원, 중첩의 정리,테브난의 정리,노튼의 정리, 밀만의 정리

*복잡한 회로를 간단한 회로로 만들기 위한 도구 또는 스킬이라고 할 수가 있다.

*중첩의 정리와 테브난의 정리를 중점으로 보자

 

*선형회로망:R,L,C,G로 이루어진 회로

*R,L,C,G를 선형소자라고 하고 전압이나 전류가 변해도 그 값이 변하지 않는 소자이다.

 

●전압원(전압의 원천)

*전압원의 내부 임피던스가 작으면 작을수록 좋다

*이상적 Z=0

 

●전류원(전류의 원천)

전류원의 부호

*전류원의 내부 임피던스가 크면 클수록 좋다

*이상적 Z=∝

 

●중첩의 정리 - 선형회로에서만 가능.전압원 전류원이 2개 이상일 때.

전압원 단락(쇼트), 전류원 개방(오픈)

*위의 회로에서 중첩의 원리를 이용하여 전류(I)를 구하여 보자.

①전압원을 제거한다......전압원 단락....전압원을 그냥 선으로 긋는다.

전압원을 제거하고 선을 그었다

*전류원에 의한 전류(I)1을 구한다.

\[ I_{_{1}}=\frac{2}{4+2}\times 6=2[A]\]

 

②전류원 제거 - 전류원 개방

전류원을 제거하고 개방 상태 즉 끊어진 상태로 그린다

전류원을 제거하고 개방 상태로 했다

*전압원에 의한 전류(I)2를 구한다

\[I_{2}=\frac{6}{2+4}=1[A]\]

 

③합친다

\[I=I_{1}+I_{2}=2+1=3[A]\]

 

●테브난의 정리

①떼어낸다

②V(th)를 구한다

③단락(전압원) 또는 개방(전류원)을 하고 단락 또는 개방한 측을 바라본다.

④R(th)를 구한다

⑤붙인다

테브난 등가회로로 변환

 

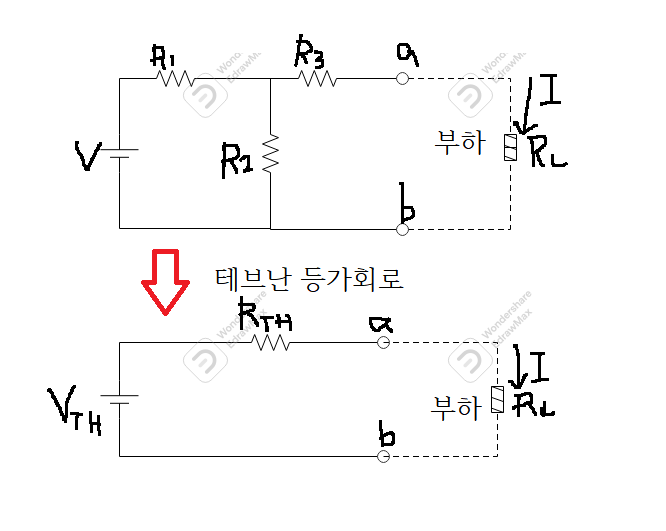
*테브난의 정리를 사용하여 부하에 흐르는 전류(I)를 구하여 보자

①떼어낸다

②V(th)를 구한다

 

부하 부분을 떼어내고 개방 상태로 한다.

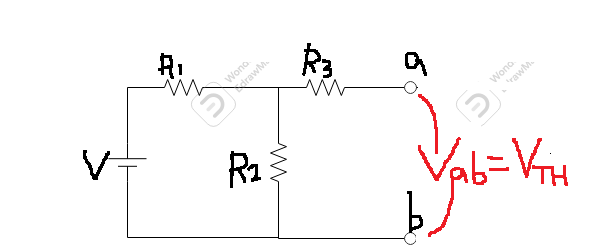
*부하 부분을 떼어내고 개방 상태로 한다

*전압 V(th)를 구한다.

\[V_{TH}=V_{ab}=\frac{R_{2}}{R_{1}+R_{2}}V\]

 

③단락(전압원) 또는 개방(전류원)을 하고 단락 또는 개방한 측을 바라본다.

전압원을 단락시킨다. 전선의 형태로 그린다.

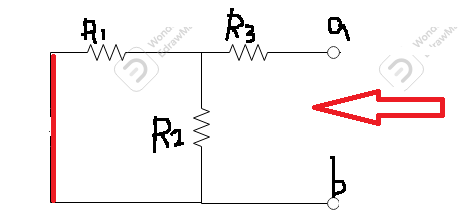
*전압원을 단락 시킨다(전선의 형태) / 만약 전류원이라면 개방(오픈)한다.

 

④R(th)를 구한다

\[R_{TH}=R_{3}+\frac{R_{1}R_{2}}{R_{1}+R_{2}}\]

 

⑤붙인다

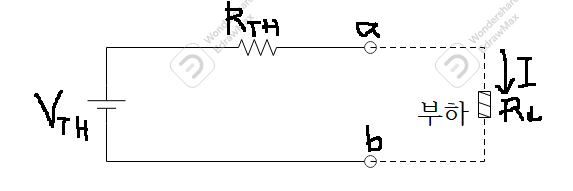
*처음에 떼어둔 부하 부분을 다시 붙인다. 그러면 테브난의 등가회로가 만들어진다. 복잡했던  회로를 간단한 회로로 등가변환한 후에 전류(I) 값을 구한다.

\[I=\frac{V_{TH}}{R_{TH}+R_{L}}\]

 

 

●노튼의 정리

복잡한 회로를 노튼의 등가회로로 간단하게 만들었다.

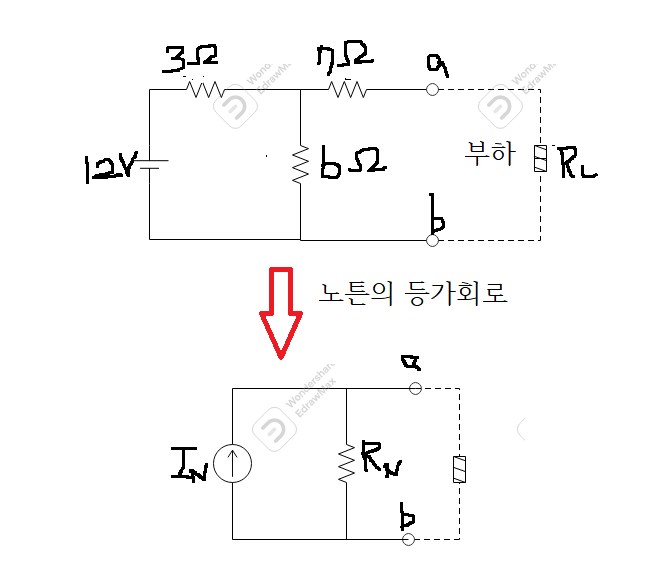
*숫자를 넣고 풀어보며 알아보자

*부하부분을 떼어내고 a,b 단자를 단락시킨다,즉 선으로 연결한다. 

*a,b사이에 흐르는 전류를 I(N)이라고 하고 그 값을 구한다.

\[ R_{T}=3+\frac{6\times 7}{6+7}=6.23[\Omega]\]

\[I_{T}=\frac{V}{R_{T}}=\frac{12}{6.23}=1.93\]

\[I_{N}=\frac{6}{6+7}\times I_{T}=\frac{6}{6+7}\times 6.23=0.89\]

 

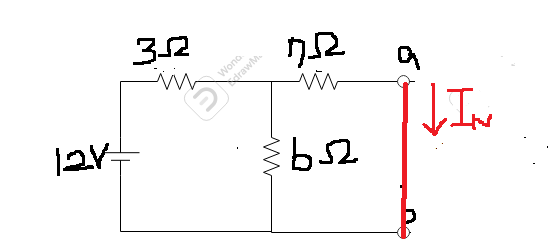
*떼어낸 부분을 개방

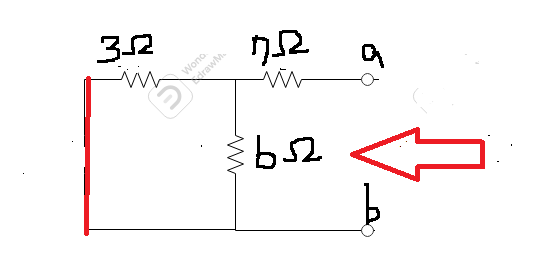
*전압원을 제거 후에 단락시킨다

*단락 또는 개방한 측을 바라본다

*R(N)을 구한다

\[R_{N}=3+6=9\Omega \]

 

 

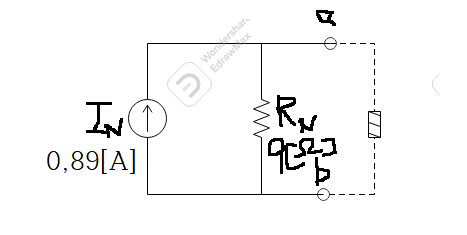
*떼어둔 부분을 다시 붙인다.

*이렇게 하면 복잡하던 회로가 간단하게 정리가 되었다.

*원하는 값을 구하면 된다

 

●밀만의 정리

\[V=IZ=\frac{I}{Y}=\frac{I_{1}+I_{2}+I_{3}...........}{Y_{1}+Y_{2}+Y_{3}..........}\]

\[=\frac{\frac{E_{1}}{Z_{1}}+\frac{E_{2}}{Z_{2}}+\frac{E_{3}}{Z_{3}}.......}{\frac{1}{Z_{1}}+\frac{1}{Z_{2}}+\frac{1}{Z_{3}}.......}\]