Y결선,델타 결선, 3상전력/회로이론

●회로이론 23강:Y결선,△(델타)결선, 3상전력

 

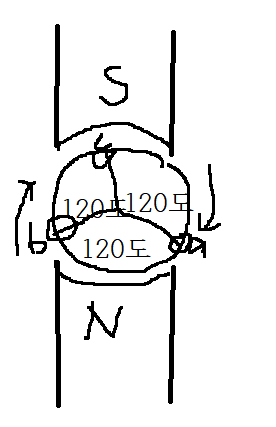
자석이 있다→자속이 나온다.

a.b.c 3가지 도체.

도체가 회전하면 자속을 끊는다.

도체가 자속을 끊을 때 기전력이 발생한다.

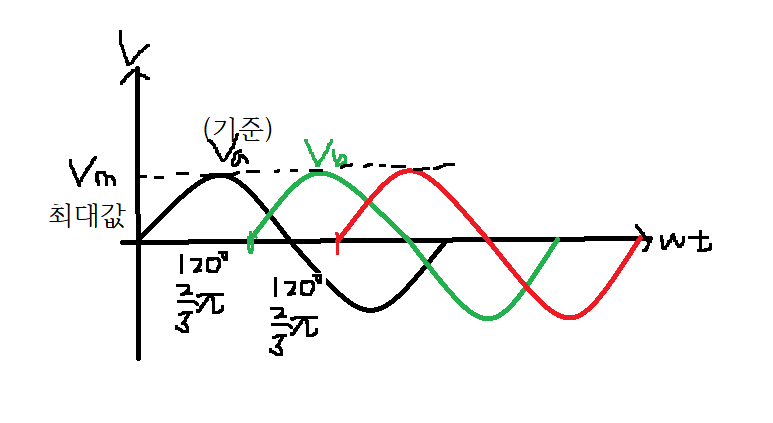
*모두 다 최대값이 같다.

*모두 다 주파수가 같다.

*각 상의 전압

$$v_m$$	최대값
V	실효값
$$v_m=\sqrt{2}V$$

$$V_a=\sqrt{2}VSin\omega t\to V\mathrm{\angle }{0}^{\circ }$$

$$V_b=\sqrt{2}VSin(\omega t-\frac{2}{3}\pi )\to V\mathrm{\angle }-\frac{2}{3}\pi$$

$$\to V\mathrm{\angle }-{120}^{\circ }\to V\mathrm{\angle }{240}^{\circ }$$

$$V_C=\sqrt{2}VSin(\omega t-\frac{4}{3}\pi )$$

$$V\mathrm{\angle }-{240}^{\circ }\to V\mathrm{\angle }{120}^{\circ }$$

$$\to V_a+v_b+v_c=0$$

 

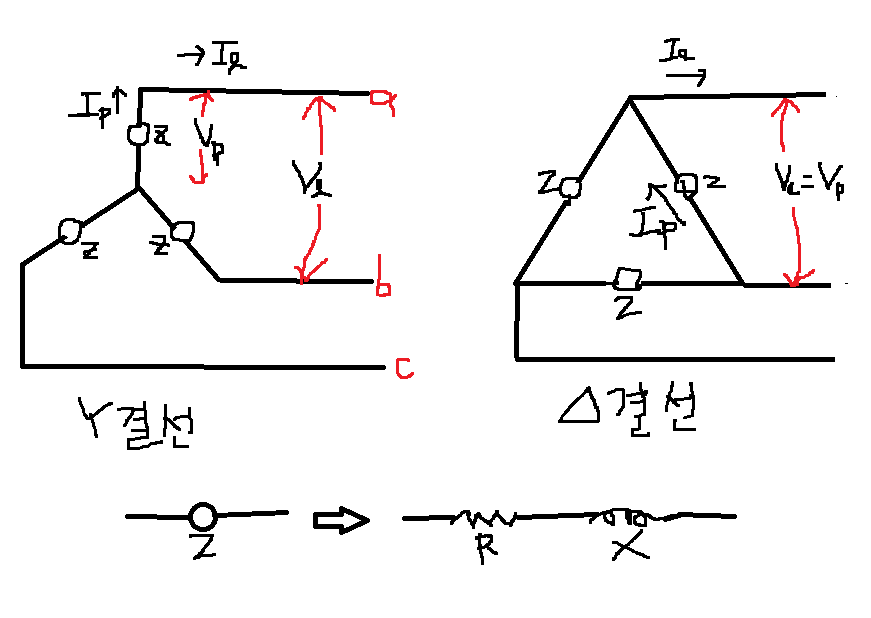
●Y결선

$$V_l$$	선간전압
$$V_p$$	상전압
$$I_l$$	선전류
$$I_p$$	상전류

 

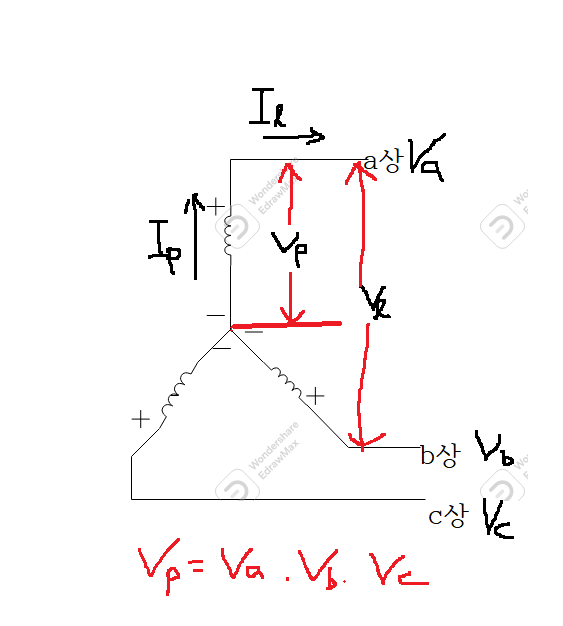
$$V_l=\sqrt{3}{V}_p\mathrm{\angle }{30}^{\circ }$$

$$I_l=I_p$$

 

●△(델타)결선

 

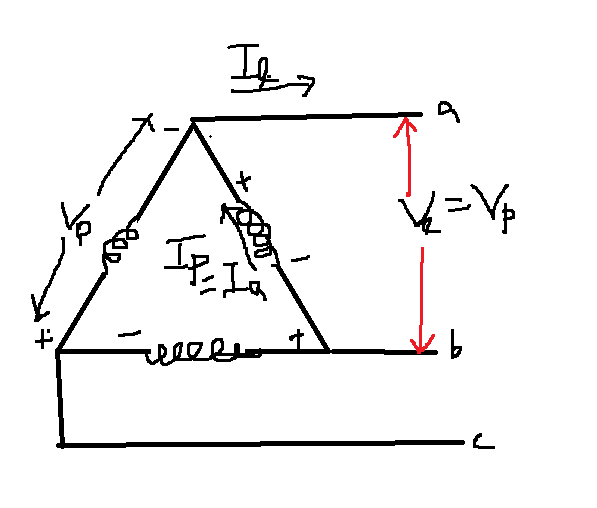
$$V_l=V_p$$

$$I_l=\sqrt{3}{I}_p\mathrm{\angle }-{30}^{\circ }$$

 

●3상전력

*유효전력

$$P=3I_p^{2}R=\frac{3V_p^{2}R}{R^2+X^2}$$

$$=3V_p{I}_{p}cos\theta [W]$$

$$=\sqrt{3}{V}_l{I}_{l}cos\theta [W]$$

 

*무효전력

$$P_r=3I_p^{2}X=\frac{3V_p^{2}X}{R^2+X^2}[V_{ar}]$$

$$=3V_p{I}_{p}sin\theta [V_{ar}]$$

$$=\sqrt{3}{V}_l{I}_{l}sin\theta [V_{ar}]$$

 

 

*피상전력

$$P_a=3I_p^{2}Z=\frac{3V_p^{2}Z}{R^2+X^2}[VA]$$

$$=3V_p{I}_p[VA]$$

$$=\sqrt{3}{V}_l{I}_l[VA]$$

 

 

●n상 Y결선

$$V_l=2sin\frac{\pi }{n}{V}_p\mathrm{\angle }\frac{\pi }{2}(1-\frac{2}{n})$$

$$I_l=I_p$$

 

●n상 △(델타)결선

$$I_l=2sin\frac{\pi }{n}{I}_p\mathrm{\angle }-\frac{\pi }{2}(1-\frac{2}{n})$$

$$V_l=V_p$$