대칭좌표법,벡터연산자, 불평형 3상회로,영상분,정상분,역삼분/회로이론

●27강:대칭좌표법,벡터연산자, 불평형 3상회로,영상분,정상분,역삼분

●3상 평형, 3상 대칭:크기가 같고 각도가 120º일 때

●벡터연산자 a =1∠120º

a·A=C

$a^{2}A=B$

$a^{3}A=A$

 

a=1 ∠ 120º

  =1(cos120º+jsin120º)

$a=-\frac{1}{2}+j\frac{\sqrt{3}}{2}$

 

$a^2=1\angle 240$º

          =1 (cos240º+jsin240º)

         $=-\frac{1}{2}-j\frac{\sqrt{3}}{2}$

 

*크기가 같고 각도가 120˚일 때 3상 평형, 3상 대칭이라고 하다.

$V_a+V_b+V_c=0$

$V_a+a^2{V}_a+a{V}_a=0$

$V_a(1+a^2+a)=0$ 

 

$1+a^2+a=1+(-\frac{1}{2}-j\frac{\sqrt{3}}{2})+(-\frac{1}{2}+j\frac{\sqrt{3}}{2})=0$ 

 

●불평형 3상 회로

●영상분-3상 동일 성분$(V_0)$

●정상분-기본파와 동일성분$(V_1)$

●역상분-기본파와 반대성분$(V_2)$

 

$V_a=V_0+V_1+V_2$

$V_b=V_0+a^2{V}_1+a{V}_2$

$V_c=V_0+a{V}_1+a^2{V}_2$

 

●영상분-3상 동일 성분$(V_0)$

$V_0=\frac{1}{3}(V_a+V_b+V_c)$

*3상평형(3상대칭)일 때는 $V_0=0$  즉, 영상분이 존재하지 않는다.

 

●정상분-기본파와 동일성분$(V_1)$

$V_1=\frac{1}{3}(V_a+a{V}_b+a^2{V}_c)$

*3상평형(3상대칭)일 때는 $V_1=V_a$ 이다.

 

●역상분-기본파와 반대성분$(V_2)$

$V_2=\frac{1}{3}(V_a+a^2{V}_b+aVc)$

*3상평형(3상대칭)일 때는 $V_2=0$ 즉, 역상분이 없다.

 

●$불평형률=\frac{역상분V_2}{정상분V_1}$........불평하면서 역정을 낸다라고 외우면 좋다

 

●사고

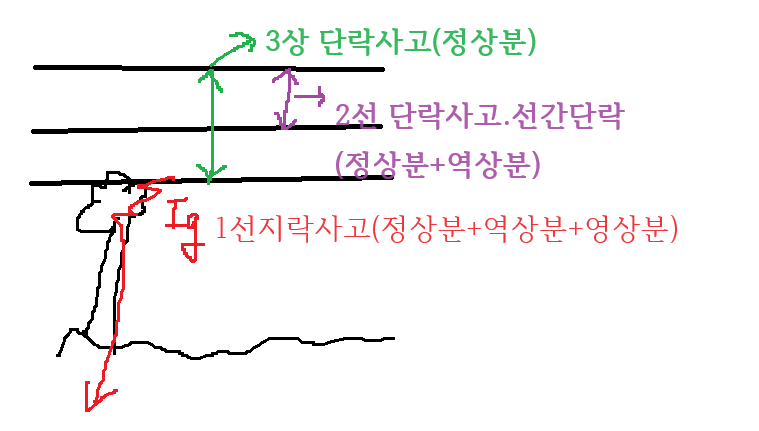
●발전기를 포함한 3상 회로의 계산

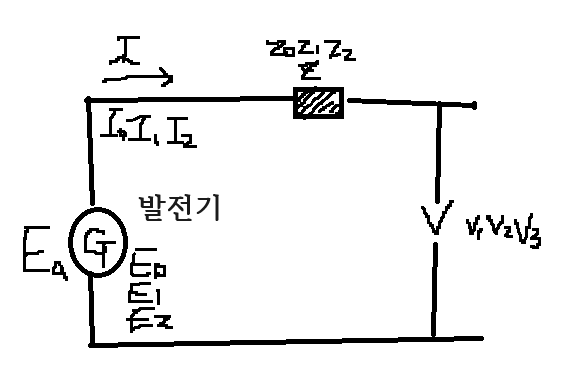
*발전기의 일반식

$V=E_a-I\cdot Z$

 

$V_0=E_0-I_0{Z}_0$

$V_1=E_1-I_1{Z}_1$

$V_2=E_2-I_2{Z}_2$

 

*3상 평형일 때 $(E_0,E_2)$가 없다. 그러므로

$V_0=-I_0{Z}_0$

$V_1=E_1-I_1{Z}_1$

$V_2=-I_2{Z}_2$