비정현파 교류, 푸리에급수,비정현파의 계산/회로이론

 

●회로이론 29강:비정현파 교류, 푸리에급수,비정현파의 계산

●비정현파 교류

*교류--정현파(sin,cos) --sin :정현파

                                     --cos : 여현파

        --비정현파--삼각파

                         --구형파

                         --왜형파

 

*비정현파=직류분+기본파+n고조파

*직류분$a_{0}$

*기본파 : 1고조파, $a_{1}cos\omega{t}$, $b_{1}sin\omega{t}$

*(n)고조파:기본파가 n번, $a_{n}cos(n\omega{t})$, $b_{n}sin(n\omega{t})$

*참고로 고주파와 고조파에 대하여 ....

고주파: 주파수(f)가 굉장히 높은 것.

고조파:w→2$\pi$f(기본파,1고조파)

            2w→$2\cdot2\pi$f(2고조파)

            3w→$3\cdot2\pi$f(3고조파)

                  .

                  .

                  .

         nw→$n\cdot2\pi$f(n고조파)

 

*비정현파를 푸리에급수로 표현해 보자.

$f(t)=a_0+a_1cos\omega{t}+a_2cos2\omega{t}......+a_ncos(n\omega{t})$

        $+b_1sin\omega{t}+b_2sin2\omega{t}+.........+b_nsin(n\omega{t})$

 

*푸리에급수의  일반식

$f(t)=a_{0}+\sum_{n=1}^{\infty}a_{n}cos(n\omega{t})+\sum_{n=1}^{\infty}b_{n}sin(n\omega{t})$

 

*적분

$a_0=\frac{1}{T}\int_{0}^{T}f(t)dt$

 

$a_{n}=\frac{2}{T}\int_{0}^{T}f(t)cos(n\omega{t})dt$

$=\frac{1}{\pi}\int_{0}^{2\pi}f(t)cos(n\omega{t})dt$

 참고로 주기 $T=2\pi$이다.

 

$b_n=\frac{2}{T}\int_{0}^{T}f(t)sin(n\omega{t})dt$

$=\frac{1}{\pi}\int_{0}^{2\pi}f(t)sin(n\omega{t})dt$

 

*원점대칭,정현파,sin파,기함수

$a_0$항과 $a_n$항은 없다.

$b_n$항(sin항)은 존재.

$f(t)=-f(-t)$

$sin30^{\circ}=-sin(-30^{\circ})$

 

*y축 대칭,여현파,cos파,우함수

$a_n$항 (cos항), $a_0$항(직류분) 존재.

$b_n$항은 없다.

$f(t)=f(-t)$

$cos30^{\circ}=cos(-30^{\circ})$

 

*반파대칭,x축대칭

$a_n$항(cos항)과 $b_n$항 존재.

$a_0$항은 없다.

$f(t)=-f(t-\frac{T}{2})$

$sin30^{\circ}=-sin(30^{\circ}-\frac{360^{\circ}}{2})$

참고로 주기 T=360도($2\pi$)이다.

 

●비정현파의 계산

비정현파=직류분+기본파+고조파

$V(t)=5+1\cdot\sqrt{2}sin\omega{t}+3\cdot\sqrt{2}sin3\omega{t}+5\cdot\sqrt{2}sin5\omega{t}[V]$

$i(t)=3+4\cdot\sqrt{2}sin(\omega{t}-30^{\circ})+7\cdot\sqrt{2}sin(5\omega{t}-60^{\circ})[A]$

*실효값($V_{rms}$)

※최대값($V_m$)을 $\sqrt{2}$로 나누면 실효값($V_rms$)이 된다.

$V_rms=\sqrt{{V_0}^{2}+(\frac{V_{m1}}{\sqrt{2}})^{2}+(\frac{V_{m2}}{\sqrt{2}})^{2}....(\frac{V_{mn}}{\sqrt{2}})^{2}}$

$V_{rms}=\sqrt{5^{2}+1^{2}+3^{2}+5^{2}}=\sqrt60$

$I_{rms}=\sqrt{3^2+4^2+7^2}=\sqrt74$

 

*왜형률($V_왜$)

$V_왜=\frac{전 고조파의 실효값}{기본파의 실효값}$

$V_왜=\frac{\sqrt{V_2^2+V_3^2+....+V_n^2}}{V_1}$

 

$V_왜=\frac{\sqrt{3^2+5^2}}{1}=\sqrt34$

 

$I_왜=\frac{\sqrt{7^2}}{4}=\frac{\sqrt49}{4}$

 

*피상전력($P_a$)

$P_a=V_{rms}\cdot I_{rms}=\sqrt60\times\sqrt74  [VA]$

 

*유효전력(P)

$P=V_0 I_0+V_1 I_1 cos\theta_1+V_2 I_2cos\theta_2........ $

  $=5\times3+(1\times4\times cos30^{\circ})+(5\times7 cos60^{\circ})$

    =■

 

*역률$cos\theta$

$\frac{P}{P_a}=\frac{■}{\sqrt60\times\sqrt74}=▲$

 

*비정현파의 임피던스(z)

$Z=R+j(\omega L-\frac{1}{\omega c})$

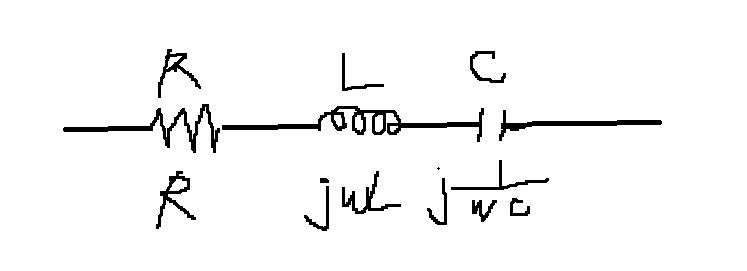
→직류분 $f=0 \,\,\,\, \omega=0 → Z_0=0$

→기본파 $\omega →Z_1\,=R+j(\omega L-\frac{1}{\omega c})$

→고조파 2: $2\omega\,→Z_2\,=R+j(2\omega L-\frac{1}{2\omega c})$

                3: $3\omega\,→Z_3\,=R+j(3\omega L-\frac{1}{3\omega c})$

                                      .

                                      .

                                      .

                 n: $n\omega\,→Z_n\,=R+j(n\omega L-\frac{1}{n\omega c})$

 

 

*공진=허수부가 0일 때 공진이라고 한다.

※$\omega=2\pi f$

 공진일 때 위의 $n\omega L-\frac{1}{n\omega c}=0$ 

$n\omega L=\frac{1}{n\omega C}$

$\omega^2=\frac{1}{n^2LC}$

$\omega=2\pi f$

$\therefore\,(2\pi f)^2=\frac{1}{n^2LC}$

$f^2=\frac{1}{(2\pi n)^2LC}$

$f=\frac{1}{2\pi n\sqrt{LC}}\,\,[HZ]$

 

*고조파의 특징

2, 3,4,5,6,7,8.........

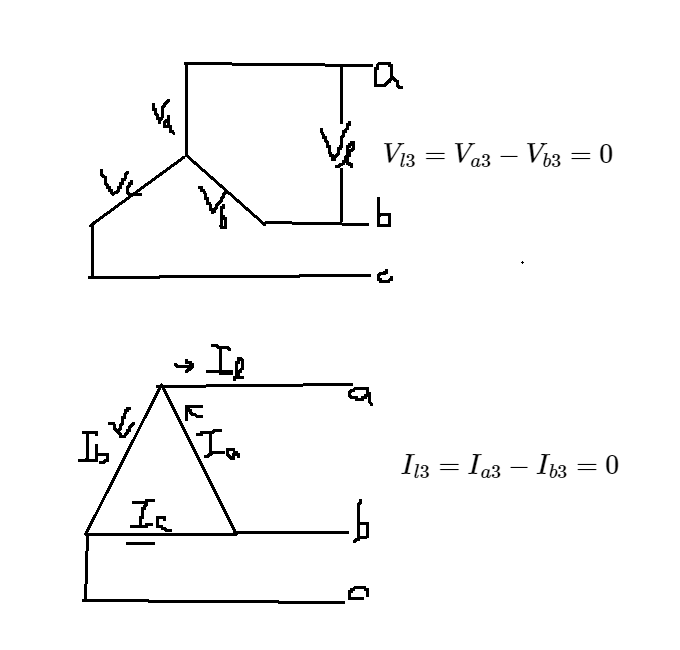
3n 고조파     3,6,9,12,15.......(a,b,c성분 동일)

3n+1 고조파 4.7.10.13.16........(상회전 동일)

3n-1 고조파 2,5,8,11,14...........(상회전 반대)

 

*$\Delta$결선 Y결선 고조파

$V_{l3}=V_{a3}-V_{b3}=0$

$I_{l3}=I_{a3}-I_{b3}=0$