4단자망(T형회로,파이형회로),Z파라미터(T형 회로),Y형 파라미터(파이형 회로)/회로이론

 

 

●회로이론 32강: 4단자망(T형회로,$\pi$형회로) ,Z파라미터(T형 회로),Y형 파라미터($\pi$형 회로)

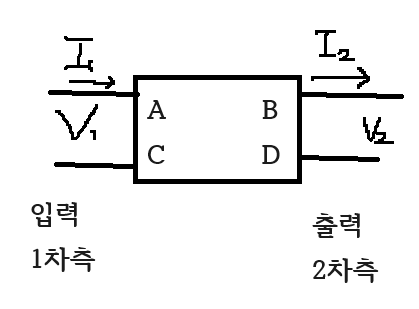
$V_1=A{V}_2+B{I}_2$

$I_1=C{V}_2+D{I}_2$

행렬식으로 나타내면...

$\left(\begin{array}{c}{V}_1\\ I_1\end{array}\right)=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)\left(\begin{array}{c}{V}_2\\ I_2\end{array}\right)$

$A=\frac{V_1}{V_2}{\mid }_{I_2=0}\to$개방   전압이득.

$B=\frac{V_1}{I_2}{\mid }_{V_2=0}\to$ 단락 임피던스.

$C=\frac{I_1}{V_2}{\mid }_{I_2=0}\to$  개방 어드미턴스.

$D+\frac{I_1}{I_2}{\mid }_{V_2=0}\to$ 단락 전류이득.

 

예시)직렬에서..

$V_1=1V_2+Z{I}_2$

$I_1=0V_2+1I_2$

$(\genfrac{}{}{0ex}{}{V_1}{I_1})=\left(\begin{array}{cc}1& Z\\ 0& 1\end{array}\right)(\genfrac{}{}{0ex}{}{V_2}{I_2})$

 

예시)병렬에서

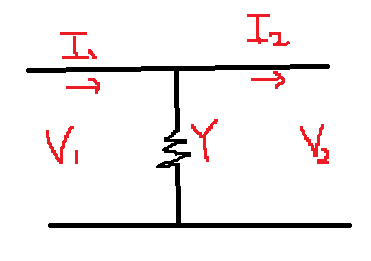
$V_1=1V_2+0I_2$

$I_1=Y{V}_2+1I_2$

$(\genfrac{}{}{0ex}{}{V_1}{I_1})=\left(\begin{array}{cc}1& 0\\ Y& 1\end{array}\right)(\genfrac{}{}{0ex}{}{V_2}{I_2})$

 

*4단자망 성질

①AD-BC=1

②A=D

 

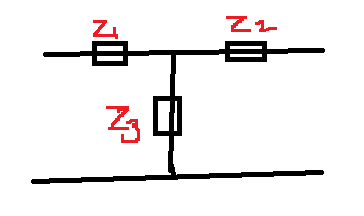
●4단자망 T형 회로

$\left(\begin{array}{cc}1& Z_1\\ 0& 1\end{array}\right)\left(\begin{array}{cc}1& 0\\ \frac{1}{Z_3}& 1\end{array}\right)\left(\begin{array}{cc}1& Z_2\\ 0& 1\end{array}\right)$

$=\left(\begin{array}{cc}1+\frac{Z_1}{Z_3}& \frac{Z_1{Z}_2+Z_2{Z}_3+Z_3{Z}_1}{Z_3}\\ \frac{1}{Z_3}& 1+\frac{Z_2}{Z_3}\end{array}\right)$

$=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)$

 

●4단자망 $\pi$형 회로

$\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)=\left(\begin{array}{cc}1+\frac{Z_2}{Z_3}& Z_2\\ \frac{Z_1+Z_2+Z_3}{Z_1{Z}_3}& 1+\frac{Z_2}{Z_1}\end{array}\right)$

 

●Z파라미터(전압을 전류로)

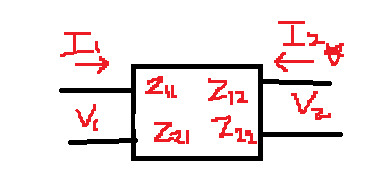
$V_1=Z_{11}{I}_1+Z_{12}{I}_2$

$V_2=Z_{21}{I}_1+Z_{22}{I}_2$

$(\genfrac{}{}{0ex}{}{V_1}{V_2})=\left(\begin{array}{cc}{Z}_{11}& Z_{12}\\ Z_{21}& Z_{22}\end{array}\right)(\genfrac{}{}{0ex}{}{I_1}{I_2})$

※위에서 $Z_{11}{Z}_{12}{Z}_{21}{Z}_{22}$를 임피던스(Z) 파라미터라고 한다.

$Z_{11}=\frac{V_1}{I_1}{|}_{I_2=0}$

$Z_{12}=\frac{V_1}{I_2}{|}_{I_1=0}$

$Z_{21}=\frac{V_2}{I_1}{|}_{I_2=0}$

$Z_{22}=\frac{V_2}{I_2}{|}_{I_1=0}$

 

●T형회로(Z파라미터)

$Z_{11}=Z_1+Z_2$

$Z_{12}=Z_3$

$Z_{21}=Z_3$

$Z_{22}=Z_2+Z_3$

 

●Y파라미터(전류을 전압으로)

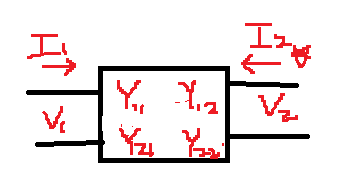
$I_1=Y_{11}{V}_1+Y_{12}{V}_2$

$I_2=Y_{21}{V}_1+Y_{22}{V}_2$

$(\genfrac{}{}{0ex}{}{I_1}{I_2})=\left(\begin{array}{cc}{Y}_{11}& Y_{12}\\ Y_{21}& Y_{22}\end{array}\right)(\genfrac{}{}{0ex}{}{V_1}{V_2})$

※위에서 $Y_{11}{Y}_{12}{Y}_{21}{Y}_{22}$를 어드미턴스(Y) 파라미터라고 한다.

$Y_{11}=\frac{I_1}{V_1}{|}_{V_2=0}$

$Y_{12}=\frac{I_1}{V_2}{|}_{V_1=0}$

$Y_{21}=\frac{I_2}{V_1}{|}_{V_2=0}$

$Y_{22}=\frac{I_2}{V_2}{|}_{V_1=0}$

 

●$\pi$형 회로(Y파라미터)

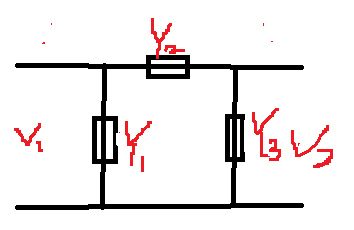
$Y_{11}=Y_1+Y_2$

$Y_{12}=-Y_2$

$Y_{21}=-Y_2$

$Y_{22}=Y_2+Y_3$

 

●이상변압기 4단자 정수

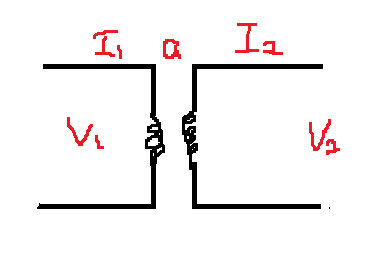
$\underset{(권수비)}{a}=\frac{V_1}{V_2}=\frac{I_2}{I_1}$

$V_1=a{V}_2+0I_2$

$I_1=0V_2+\frac{1}{a}{I}_2$

$\left(\begin{array}{cc}a& 0\\ 0& \frac{1}{a}\end{array}\right)$