●회로이론 35강:라플라스 변환,라플라스재정리
●표로 정리


● 라플라스 변환의 정의
$F_{(S)}$= ℒ[f(t)](s)= $\int_{0}^{\infty}f(t)\cdot e^{-st}\cdot dt$
●단위계단함수
$f(t)=u(t)$
$u(t)\left\{\begin{matrix}0<t\,\,\,\to\,\,\,1\\0>t\,\,\,\to\,\,\,0\end{matrix}\right.$
F(s)= ℒ[u(t)](s)=$\frac{1}{S}$
F(s)= ℒ[3$\cdot$ u(t)](s)=$3\frac{1}{S}$
●단위 임펄스함수(단위충격함수).델타함수
$f(t)=\delta(t)$
$f(s)=ℒ[\delta(t)](s)=1$
$f(t)=1, (t=0)$
$f(t)=0, (t≠0)$
●단위경사함수
$f(t)=t$
$f(t)=t\cdot u(t)$
F(s)= ℒ $[t\cdot u(t)](s)=\frac{1}{S^2}$
●상수 함수
$f(t)=K$ F(s)= ℒ[k](s)=$k\frac{1}{S}$
●시간의 함수
$f(t)=t^n$
$F(s)$= ℒ $[t^n]=\frac{n!}{S^{n+1}}$
※!(팩토리얼) 앞의 숫자부터 아래로 1까지 곱한다는 의미이다. 예를들면 5!=5× 4× 3 ×2 ×1 이다.
예시)
$f(t)=t^4$
$F(s)$=$[t^4](s)=\frac{4!}{S^{4+1}}=\frac{24}{S^5}$
※4!=4 × 3 × 2 × 1=24
●지수 함수
$f(t)=e^{-at}$
$f(t)=e^{at}$
$F(s)$= ℒ$[e^{-at}](s)=\frac{1}{s+a}$
$F(s)$= ℒ$[e^{at}](s)=\frac{1}{s-a}$
●삼각 함수
$f(t)=sin\omega t$
$f(t)=cos\omega t$
$F(s)$= ℒ$[sin\omega t](s)=\frac{\omega}{S^2+\omega^2}$
$F(s)$= ℒ$[cos\omega t](s)=\frac{S}{S^2+\omega^2}$
●쌍곡선 함수
$f(t)=sinh\omega t$
$f(t)=cosh\omega t$
$F(s)$= ℒ$[sinh\omega t](s)=\frac{\omega}{S^2-\omega^2}$
$F(s)$= ℒ$[cosh\omega t](s)=\frac{S}{S^2-\omega^2}$
● ● 라플라스 재정리 ● ●
●시간추이 정리
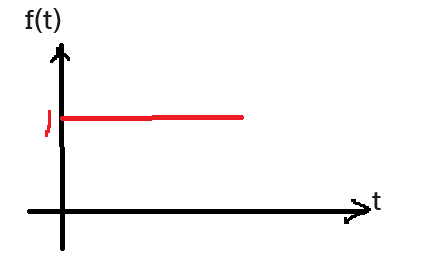
$f(t)=u(t)\,\,\,\overset{라플라스 변환}{\rightarrow}\frac{1}{S}$
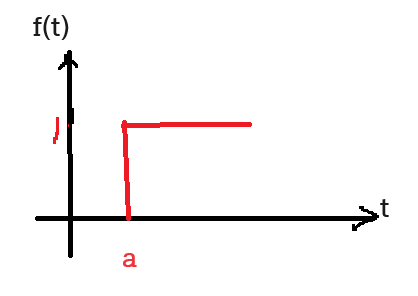
$f(t)=u(t-a)\,\,\,\overset{라플라스 변환}{\rightarrow}\frac{1}{S}e^{-as}$
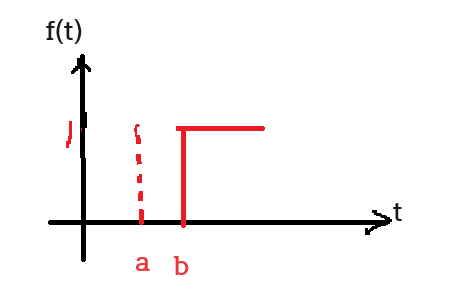
$f(t)=u(t-b)\,\,\,\overset{라플라스 변환}{\rightarrow}\frac{1}{S}e^{-bs}$
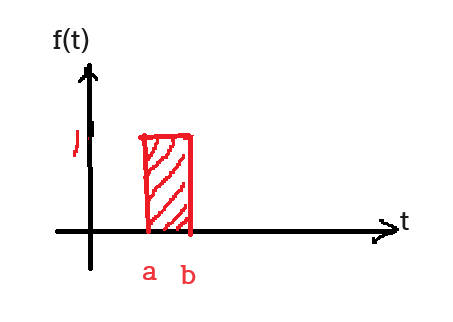
$f(t)=u(t-a)-u(t-b)\overset{라플라스 변환}{\rightarrow}$
$\frac{1}{S}(e^{-as}-e^{-bs})$
●복소추이 정리
$f(t)\cdot e^{-at}$
$F(s)$= ℒ$[ f(t)\cdot e^{-at} ](s)=F(S)|_{S\to s+a}$
예제)
$t\cdot e^{-at}$를 라플라스 변환하라
ℒ$[ t\cdot e^{-at} ](s)=\frac{1}{S^2}|_{s\to s+a}$
$=\frac{1}{(s+a)^2}$
예제)
$sin\omega t\cdot e^{-at}$를 라플라스변환하라.
$\frac{\omega}{S^2+\omega^2}|_{s\to s+a}$
$=\frac{\omega}{(s+a)^2+\omega^2}$
예제)
cos\omega t\cdot e^{at}를 라플라스 변환하라
$\frac{s}{s^2+\omega^2}|_{s\to s-a}$
$={s-a}{(s-a)^2+\omega^2}$
●복소 미분정리
$f(t)\cdot t^n\overset{라플라스변환}{\rightarrow}$
ℒ$[f(t)\cdot t^n](s)$
$=(-1)^n\frac{d^n}{ds^n}F(s)$
예제1)
$t\cdot e^{-at}$
ℒ$[t\cdot e^{-at}](s)=(-1)^1\frac{d}{ds}\,\frac{1}{s+a}$
$=\frac{1}{(s+a)^2}$
※$(\frac{f}{g})'=\frac{f'g-fg'}{g^2}$
예제2)
$t\cdot sin\omega t$
$(-1)^1\frac{d}{ds}\frac{\omega}{s^2+\omega^2}$
$(-1)\frac{0(s^2+\omega^2)-\omega\cdot 2s}{(s^2+\omega^2)^2}$
$=-\frac{-2\omega s}{(s^2+\omega^2)^2}$
$=\frac{2\omega s}{ (s^2+\omega^2)^2 }$
●실미분정리
ℒ$[\frac{d}{dt}\cdot f(t)](s)=s\cdot F(s)-F(0)$
예제)
ℒ$[\frac{d}{dt}\cdot cos\omega t](s)$
→ ℒ$[-\omega sin\omega t](s)$
→$-\omega\frac{\omega}{s^2+\omega^2}$
→$-\frac{\omega^2}{S^2+\omega^2}$
******
→ ℒ$[-\omega sin\omega t](s)$
→$S\cdot \frac{s}{s^2+\omega^2}-1$
→$\frac{S^2}{S^2+\omega^2}-\frac{S^2+\omega^2}{S^2+\omega^2}$
→$-\frac{\omega^2}{S^2+\omega^2}$
예제)
$\frac{d}{dt}x(t)+x(t)=2$
$S\cdot X(s)-x(0)+x(s)=\frac{2}{s}$
$S\cdot X(s)+x(s)=\frac{2}{s}$
$xs(s+1)=\frac{2}{s}$
$xs=\frac{2}{s(s+1)}$
●실적분정리
ℒ$[f(t)dt](s)\to\frac{1}{s}\cdot F(s)+\frac{1}{s}\cdot F(0)$
※위에서 $\frac{1}{s}cdot F(0)$은 초기값이고 $\int_{-\infty}^{0}f(t)dt$이다.
※아래는 실미분,실적분에서 많이 사용하는 것이다,
$\frac{d}{dt}\to S$
$\int dt\to\frac{1}{s}$
$f(t)\to F(S)$
$K\to\frac{k}{s}$
예제)
$e(t)=Ri(t)+L\frac{di(t)}{dt}+\frac{1}{c}\int i(t)dt\,,f(0)=0$을 라플라스변환하라.
↓ ↓ ↓ 라플라스 변환 ↓ ↓ ↓
$E(s)=R\cdot I(s)+L\cdot SI(s)+\frac{1}{c}\frac{1}{s}I(s)$
$I(s)=\frac{1}{R+SL+\frac{1}{sc}}E(s)$
$=\frac{sc}{S^2LC+SRC+1}E(s)$
●초기값정리
$f(0+)=\displaystyle\lim_{t\to 0}f(t)=\displaystyle\lim_{s\to\infty}S\cdot F(s)$
예제)
$I(s)=\frac{2(S+1)}{S^2+2S+5}$
↓ ↓ ↓ 초기값정리 ↓ ↓ ↓
$\displaystyle\lim_{s\to\infty}S\frac{2(S+1)}{S^2+2S+5}$
$\displaystyle\lim_{s\to\infty}\frac{2S^2+2S}{S^2+2S+5}$여기에서 분자,분모에서 각 각 $\times\frac{1}{S^2}$를 하면
$=\frac{2+\frac{2}{S}}{1+\frac{2S}{S^2}+\frac{5}{S^2}}=2$
●최종값정리
$f(\infty)=\displaystyle\lim_{t\to\infty}f(t)=\displaystyle\lim_{s\to0}S\cdot F(s)$
예제)
$C(c)=\frac{5}{S((S^2+S+2)}$
↓ ↓ ↓ 최종값정리 ↓ ↓ ↓
$\displaystyle\lim_{s\to0}S\cdot\frac{5}{S(S^2+S+2)}=\frac{5}{2}$
'전기(산업)기사필기 > 회로이론' 카테고리의 다른 글
| 전달함수,전기기사 회로이론 (2) | 2023.11.01 |
|---|---|
| 과도현상,R-L직렬,R-C직렬,R-L-C직렬,L-C직렬,전기기사회로이론 (0) | 2023.10.27 |
| 영상임피던스, 영상전달정수, 분포정수회로, 무손실, 무왜형, 정재파, 회로이론 (0) | 2023.09.30 |
| 4단자망(T형회로,파이형회로),Z파라미터(T형 회로),Y형 파라미터(파이형 회로)/회로이론 (0) | 2023.09.29 |
| 2단자망,영점및 극점, 정저항회로, 역회로/회로이론 (0) | 2023.09.27 |



