벡터의 연산,더하기,빼기,내적,외적,기울기,발산,회전,전기자기학(전기기사)

●전기자기학 1-1장:벡터의 연산

● +,- ,×(내적,외적),미분(기울기,발산,회전)

●더하기(같은 성분끼리 더한다)

$\overrightarrow{A}=6i+7j+8k$

$\overrightarrow{B}=3i+4j+5k$

$\overrightarrow{A}+\overrightarrow{B}$

$=i(6+3)+j(7+4)+k(8+5)$

$=9i+11j+13k$

 

●빼기(같은 성분끼리 뺀다)

$\overrightarrow{A}=6i+7j+8k$

$\overrightarrow{B}=3i+4j+5k$

$=i(6-3)+j(7-4)+k(8-5)$

$=3i+3j+3k$

 

●내적(스칼라곱)=일

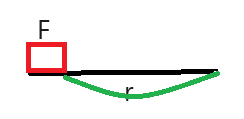
w=F×r

일=힘×거리

$\overrightarrow{A}\circ \overrightarrow{B}=ABcos\theta$

※$\circ$는 '도트'라고 읽는다.

$\cos \theta \{\begin{array}{c}{0}^{\circ }=1\\ {90}^{\circ }=0\end{array}$

$i\circ i=j\circ j=k\circ k=1$

$i\circ j=j\circ k=k\circ i=0$

$\overrightarrow{A}=Axi+Ayj+Azk$

$\overrightarrow{B}=Bxi+Byj+Bzk$

$\overrightarrow{A}\circ \overrightarrow{B}$

$=(Axi+Ayj+Azk)\circ (Bxi+Byj+Bzk)$

$=AxBx+AyBy+AzBz$

위와 같이 내적은 스칼라이고 같은성분끼리 곱한다.(i,j,k는 없다.)

 

●외적(벡터곱).회전면적

$\overrightarrow{A}\times \overrightarrow{B}=ABsin\theta \overrightarrow{n}$

※$\times$는 '크로스'라고 읽고, $\overrightarrow{n}$은 법선벡터(수직벡터).

$i\times i=j\times j=k\times k=0$

$i\times j=k$

$j\times k=i$

$k\times i=j$

$j\times i=-k$

$k\times j=-i$

$i\times k=-j$

※방향이 중요하다.

※내적은 같은 성분끼리.

※외적은 수직 성분끼리.

※행렬로 계산하면 좋다.

 

$\overrightarrow{A}=Axi+Ayj+Azk$

$\overrightarrow{B}=Bxi+Byj+Bzk$

$\overrightarrow{A}\times \overrightarrow{B}=?$

$\downarrow$행렬로 계산하면.

$\left[\begin{array}{ccc}i& j& k\\ Ax& Ay& Az\\ Bx& By& Bz\end{array}\right]$

$=i(AyBz-AzBy)+j(AzBx-AxBz)+k(AxBy-AyBx)$

 

ex)$\overrightarrow{A}\circ \overrightarrow{B}$

$(2i+3j-4k)\circ (3i+j+2k)$

=6+3-8

=1

ex)$\overrightarrow{A}=3i-3j+2k$

$\overrightarrow{B}=4i+2j-3k$

$\overrightarrow{A}\times \overrightarrow{B}=?$

$\left[\begin{array}{ccc}i& j& k\\ 3& -3& 2\\ 4& 2& -3\end{array}\right]$

$=i(9-4)+j(8+9)+k(6+12)$

$=5i+17j+18k$

 

●미분에 대해서

$x^n$를 미분하면 $n{x}^{n-1}$

 

$\frac{d}{dx}{x}^2=2x$

 

※$x$에 대한 미분일 때,$x$외에 다른 거는 그대로...

 

$\frac{d}{dx}{x}^{2}yz=2xyz$

 

※$x$에 대해 미분할 때, $x$가 없으면 '0'이다.

 

$\frac{d}{dx}{y}^{2}z$=0

 

$\frac{d}{dx}(x^{3}yz+y^{2}z=3x^{2}yz+0)$

 

●벡터의 미분(기울기,발산,회전)

 역삼각형 $▽$ 을 '나블라'라고 읽고, 그 의미는 아래와 같다.

$▽=\frac{\partial }{\partial x}i+\frac{\partial }{\partial y}j+\frac{\partial }{\partial z}k$

※$\partial$을 '라운드'라고 읽는다.

 

●기울기,경도(grad,그라디언트)

$▽\overrightarrow{A}$:grad('그라디언트'라고 읽는다.),기울기

 

$\overrightarrow{A}=Axi+Ayj+Azk$

 

$▽\overrightarrow{A}=(\frac{\partial }{\partial x}i+\frac{\partial }{\partial y}j+\frac{\partial }{\partial z}k)\overrightarrow{A}$

 

$=\frac{\partial }{\partial x}\overrightarrow{A}i+\frac{\partial }{\partial y}\overrightarrow{A}j+\frac{\partial }{\partial z}\overrightarrow{A}k$

 

●발산(div,다이버전스) :태양처럼 퍼져나가는 양,스칼라

 

$div\overrightarrow{A}=▽\circ \overrightarrow{A}$

 

$div\overrightarrow{A}=▽\circ \overrightarrow{A}$

 

$=(\frac{\partial }{\partial x}i+\frac{\partial }{\partial y}j+\frac{\partial }{\partial z}k)\circ (Axi+Ayj+Azk)$

 

$=\frac{\partial }{\partial x}Ax+\frac{\partial }{\partial y}Ay+\frac{\partial }{\partial z}Az$

 

ex)$vecV=x^{2}yz$,(3,2,1)일 때

 

$▽\overrightarrow{V}=?$

 

$=\frac{\partial }{\partial x}\overrightarrow{V}i+\frac{\partial }{\partial y}\overrightarrow{V}j+\frac{\partial }{\partial z}\overrightarrow{V}k$

 

$=\frac{\partial }{\partial x}{x}^{2}yzi+\frac{\partial }{\partial y}{x}^{2}yzj+\frac{\partial }{\partial x}{x}^{2}yzk$

 

$=2xyz+x^{2}zj+x^{2}yk$

 

↓(3,2,1) 즉 $x=3,y=2,z=1$을 대입하면

 

$=12i+9j+18k$

 

ex)$vecV=x{y}^{2}i+yzj+xzk$(3,2,1)일 때

 

$div\overrightarrow{V}=?$

 

$=\frac{\partial }{\partial x}Vx+\frac{\partial }{\partial y}Vy+\frac{\partial }{\partial z}Vz$

 

$=\frac{\partial }{\partial x}x{y}^2+\frac{\partial }{\partial y}yz+\frac{\partial }{\partial z}xz$

 

$=y^2+z+x$

 

↓(3,2,1) 즉 $x=3,y=2,z=1$을 대입하면

 

$=4+1+3$

 

$=8$

 

●회전(rot,curl)

$▽\times \overrightarrow{A}$

 

$=(\frac{\partial }{\partial x}i+\frac{\partial }{\partial y}j+\frac{\partial }{\partial z}k)\times (Axi+Ayj+Azk)$

 

$\left[\begin{array}{ccc}i& j& k\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\\ Ax& Ay& Az\end{array}\right]$

 

$=i(\frac{\partial }{\partial y}Az-\frac{\partial }{\partial z}Ay)+j(\frac{\partial }{\partial z}Ax-\frac{\partial }{\partial x}Az)+k(\frac{\partial }{\partial x}Ay-\frac{\partial }{\partial y}Ax)$

 

●$▽\circ ▽={▽}^2$

※라블라도트라블라는 라플라시안

※미분도트미분은 2번 미분

 

●$▽\times ▽=0$

※라블라 클로스 라블라=0(기울기의 회전=0)

 

●스토크의 정리

$\int \overrightarrow{A}\cdot dl=\int ▽\times \overrightarrow{A}ds$

 

●발산 정리

$\int E\cdot ds=\int divEdv$