기초수학,삼각함수,피타고라스정리,미분적분,전기자기학(전기기사)

●전기자기학 기초수학:삼각함수,미분 적분.

 

●삼각함수

$sin\theta =\frac{b}{c}\to b=csin\theta$

 

$cos\theta =\frac{a}{c}\to a=ccos\theta$

 

$tan\theta =\frac{b}{a}=\frac{sin\theta }{cos\theta }$

 

 

$\theta$	$0^{\circ }$	${30}^{\circ }$	${45}^{\circ }$	${60}^{\circ }$	${90}^{\circ }$
$sin\theta$	0	$\frac{1}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{\sqrt{3}}{2}$	1
$cos\theta$	1	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{2}$	0
$tan\theta$	0	$\frac{1}{\sqrt{3}}$	1	$\sqrt{3}$	$\mathrm{\infty }$

 

 

●피타고라스 정리

$a^2+b^2=c^2$

※위 삼각함수 그림에서 c=1이라면 $b=sin\theta /,/,c=cos\theta$가 된다. a와b를 대입하면

$c^{2}co{s}^2\theta +c^{2}si{n}^2\theta =c^2$

$co{s}^2\theta +si{n}^2\theta =1$

 

 

 

*위의 삼각형에서 sin은 y축이고, cos은 x축이다. 그러므로 각 사분면의 sin과 cos의 부호는 위의 그림과 같다.

*먼저 부호부터 정리를 해야한다.

1사분면	$sin\theta$(+)
	$cos\theta$(+)
2사분면	$sin\theta$(+)
	$cos\theta$(-)
3사분면	$sin\theta$(-)
	$cos\theta$(-)
4사분면	$sin\theta$(-)
	$cos\theta$(+)

 

*2사분면일 때는 부호는 그대로, sin과 cos이 바뀐다.

$sin({90}^{\circ }+\theta )=+cos\theta$

$cos({90}^{\circ }+\theta )=-sin\theta$

 

*3사분면일 때는 모두 다 그대로 간다.

$sin({180}^{\circ }+\theta )=-sin\theta$

$cos({180}^{\circ }+\theta )=-cos\theta$

 

보기)

$sin{120}^{\circ }\to sin({90}^{\circ }+{30}^{\circ })\to +cos{30}^{\circ }=\frac{\sqrt{3}}{2}$

$cos{240}^{\circ }\to cos({180}^{\circ }+{60}^{\circ })\to -cos{60}^{\circ }=-\frac{1}{2}$

 

●미분과 적분

*미분의 미는 미세하다는 의미이고, 분은 나누다라는 뜻이다.

*미분:미세하게 나눈 부분→기울기,변하량

 

*적분의 적은 쌓는다는 의미이다.

*적분:미세한 부분을 쌓는 것 →면적, 체적

 

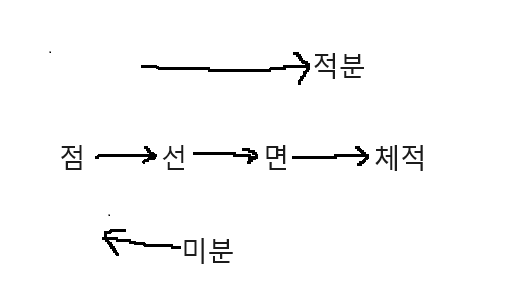
● 미분:$\frac{df(x)}{dx}\to \frac{d}{dx}f(x)\to f(x{)}^{\prime }$

 

*$\frac{d}{dx}{x}^n\to n.x^{n-1}$

 

$x^0$의 미분=1이고, 상수의 미분=0

 

예)$x^3\to 3x^2\to 3.2x^1\to 6\to 0$(연속해서 미분한 것)

 

 

● 적분:$\int f(x).dx$

 

예)$\int 6x^0.dx\to 6.\frac{1}{0+1}{x}^1\to 6.\frac{1}{2}{x}^2\to 3.\frac{1}{3}{x}^3$(연속해서 적분한 것)

 

● 로그함수

 

*$\frac{1}{x}=x^{-1}$

 

※$2^x=3\to x=lo{g}_2^3$

 

※${10}^x=3\to x=lo{g}_{10}^3$를 상용로그라 하고 $=log3$이라 한다.

 

※$e^x=3\to x=lo{g}_e^{(}3)=l_{n}3$e는 자연상수.

 

$\int \frac{1}{x}dx=l_{n}x=lo{g}_e^x$

 

$l_{n}1=0$

 

$l_{n}ab=l_{n}a+l_{n}b$

 

$l_n\frac{a}{b}=l_{n}a-l_{n}b$

 

$l_n{b}^a=a.l_{n}b$

 

● 삼각함수 미분

$\frac{d}{dx}sinx\to cosx$

 

$\frac{d}{dx}cosx\to (-)sinx$

 

● 삼각함수 적분

 

$\int sinx.dx\to (-)cosx$

 

$\int cosx.dx\to sinx$