●전기자기학 5강:전기력선,가우스법칙,포아송방정식
●전기력선:어떤 공간 상에 전계의 세기와 방향을 가상적으로 나타낸 선, 전계의 세기가 우리 눈에 보이지 않기 때문에 가상의 선으로 나타낸 것.
*전속: 전기력선의 모음

★전기력선(전계의 세기)의 특징.
①전하가 없는 곳에서는 전기력선이 발생하지도 않고 소멸하지도 않고 연속적이다.
$\triangledown.E=0$(다이브젠스.E=0)
→도체 내부에서는 전하가 없다, 전기력선도없고 전계의 세기 E=0
② + → -
③전기력선은 높은 전위(V) → 낮은 전위(V)
$\vec{E}=-\triangledown.V$
④전기력선 방향 = 전계 방향.
⑤전기력선의 밀도 = 전계의 세기
$\frac{N}{S}=E\to N=\oint{E}ds$
※N=전기력선, S=면적.
⑥Q[C]의 전하에서 $N=\frac{Q}{\epsilon_{0}}$
⑦전기력선은 자신만의 폐곡선이 되지 않는다.

$\triangledown\times{E}=0$
⑧서로 다른 전기력선은 서로 교차하지 않는다.
⑨전기력선은 등전위면과 항상 수직이다.
●전기력선 방정식
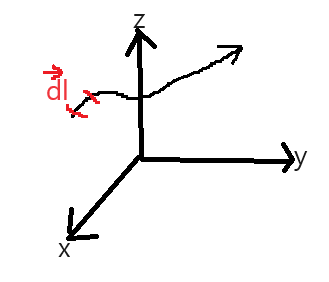
$\vec{E}=E_{xi}+E_{yj}+E_{zk}$
${\color{Red}\frac{dx}{E_x}=\frac{dy}{E_y}=\frac{dz}{E_z}}$
※예제를 보며 외운다.
ex1)${\color{Red}E=xi+yj}$(4.3.0)
${\color{Red}\to y=Ax}$
$A=\frac{y}{x}=\frac{3}{4}\to {\color{Red}y=\frac{3}{4}x}$
ex2) ${\color{Red}E=xi-yj}$(4.3.0)
${\color{Red}y=\frac{A}{x}}$
$A=xy=12$
$y=\frac{12}{x}$
●전계에서의 가우스법칙.

*가우스법칙:폐곡면 내에 전하와 폐곡면을 통과하는 전기력선과의 관계를 수학적으로 표현한 것을 말한다.
● 전하 밀도
*선전하밀도($\rho_l$)
$Q=\int\lambda.dl[c/m]$
*면전하밀도($\rho_s$)
$Q=\int{S}.ds[c/m^2]$
*체적전하밀도($\rho_v$)
$Q=\int\rho_v.dv[c/m^3]$
● 가우스법칙
전기력선 밀도=전계의 세기
*가우스의 법칙 (적분형)
$N=\oint{E}ds=\frac{Q}{\epsilon_0}$
*가우스의 법칙 (적분형)
$\triangledown.D=\rho_v$
※D(전속밀도)=$\epsilon_0{E}$
● 포아송 방정식
$\triangledown.E=\frac{\rho_v}{\epsilon_0}$
$\triangledown^2.V=-\frac{\rho_v}{\epsilon_0}$......포아송방정식
여기서$\rho_v=0$이라면
$\triangledown^2.V=0$.........라플라스 방정식
※$\triangledown^2$....라플라시안
*아래 예시를 잘 보자.
ex)$V=3x^2+2y^2+z^2$에서 $\rho_v=?$
$\triangledown^2V=\frac{\rho_v}{\epsilon_0}$
$=6+4+2=12$
$12=-\frac{\rho_v}{\epsilon_0}$
$\rho_v=-12[c/m^3]$
● 전속과 전속밀도
전속:전하와 같다고 본다
전속밀도: 단위당 전속 $D[C/m^2]$
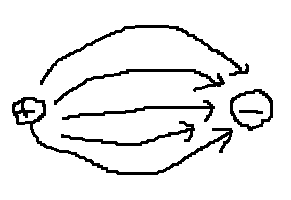
전기력선$\to\,\,\frac{Q}{\epsilon_0}$개
전속(전기력선의 묶음) → Q개
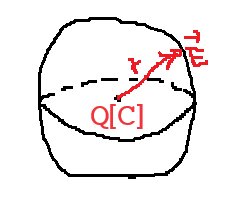
$D=\frac{Q}{4\pi{r^2}}$
위에서 분모 분자에 각 각 $\epsilon_0$를 곱한다.
${\color{Red}D=\frac{Q}{4\pi{r^2}}=\epsilon_0{E}}$
*정리*
정전력 $F=\frac{1}{4\pi{\epsilon_0}}\times\frac{Q_1.Q_2}{r^2}[N]$
↓F=Q.E
전계의 세기 $E=\frac{1}{4\pi{\epsilon_0}}\times\frac{Q}{r^2}[V/m]$
↓$E=-\triangledown{V}\,\,\,,V=-\int{E}.dr$
전위 $V=\frac{Q}{4\pi\epsilon_0r}[V]$
전속밀도 $D=\frac{Q}{4\pi{r^2}}[C/m^2]$
※ 전계의 세기 $E=\frac{1}{4\pi{\epsilon_0}}\times\frac{Q}{r^2}[V/m]$
↓$D=\epsilon_0{E}$
전속밀도 $D=\frac{Q}{4\pi{r^2}}[C/m^2]$
*$\oint{E}.ds=\frac{Q}{\epsilon_0}$(적분)
*$\triangledown.D=\rho_v$(미분)
*$\triangledown\times{E}=0$
*$\triangledown^2.V=-\frac{\rho_v}{\epsilon_0}$
*$\triangledown^2.V=0$
'전기(산업)기사필기 > 전기자기학' 카테고리의 다른 글
| 정전계,쿨롱의 법칙,정전력,전계의 세기,전위,등전위면,도체의 성질,전기자기학(전기기사) (0) | 2023.12.10 |
|---|---|
| 기초수학,삼각함수,피타고라스정리,미분적분,전기자기학(전기기사) (2) | 2023.12.03 |
| 원자의 구조,전하량,전기자기학(전기기사) (0) | 2023.12.01 |
| 벡터의 연산,더하기,빼기,내적,외적,기울기,발산,회전,전기자기학(전기기사) (0) | 2023.11.10 |
| 벡터와스칼라,성분벡터(기본벡터),단위벡터,직교좌표,직각좌표,원통좌표,구형좌표,전기자기학(전기기사) (0) | 2023.11.07 |



