●전기자기학 :정전계,쿨롱의 법칙,정전력,전계의 세기,전위.등전위면,도체의 성질
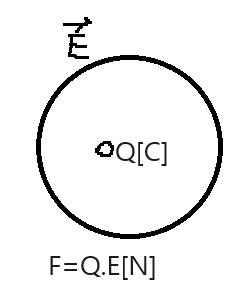
●정전계:정지되어 있는 전하의 힘이 미치는 공간.
*정전계의 특징
①에너지 분포가 최소인 상태
②가장 안정적 상태
*원자의 구조

*외부의 힘에 의해 이탈한 자유전하는 구속력이 약해져 움직일 수가 있다. 운동을 시작하는 것이다.
*전자의 운동 속도

$w=Q.V$
$=e.V$
$=\frac{1}{2}mv^2$
※$m[kg]\,\,\,v[m/s]$,V=전위, m=질량,$v$=속도, e= 전자 1개
$v=\sqrt\frac{2.e.V}{m}$
$e=1.602\times 10^{-19}[C]$
$m=9.1055\times 10^{-31}[kg]$
${\color{Red}v=5.931\times 10^{5}\sqrt V[m/s]}$
${\color{Red}\therefore \,\,\,v\propto\sqrt V}$
*유전율$\epsilon[F/m]$:전하를 잡아줄 수 있는 비율.
$\epsilon=\epsilon_0.\epsilon_s$
※$\epsilon_0$:공기나 진공 중에서의 유전율이고 값은 정해져 있다.
${\color{Red}\frac{10^{-9}}{36\pi}=8.855\times10^{-12}[F/m]}$
※$\epsilon_s$:비유전율.
●쿨롱의 법칙
*정전력 $\vec{F}[N]$ : 정지된전하들 사이에 작용하는 힘.

+ ← 반발력 → + (같은 극성)
+ ← 흡입력 → - (다른 극성)
$\vec{F}=\frac{1}{4\pi\epsilon_0}\times\frac{Q_1.Q_2}{r^2}[N]$
(+)값은 반발력.
(-)값은 흡입력.
*쿨롱 상수 K
$K=\frac{1}{4\pi\epsilon_0}=9\times10^9$
●전계의 세기$\vec{E}[V/m]$

*$\vec{E}=\frac{1}{4\pi\epsilon_0}\times\frac{Q.1}{r^2}$
여기서 1은 생략 가능 하므로
${\color{Red}\vec{E}=\frac{1}{4\pi\epsilon_0}\times\frac{Q}{r^2}}$
$F=\vec{E}.1$
$Q_1$에 미치는 힘은
$F=\vec{E}.Q_1$
● 전기력선
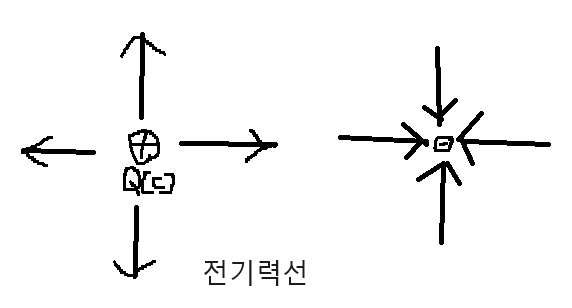
전계의 세기의방향
*전기력선:보이지 않는 것을 가상으로 그린 화살표.
●전위V[V볼트]
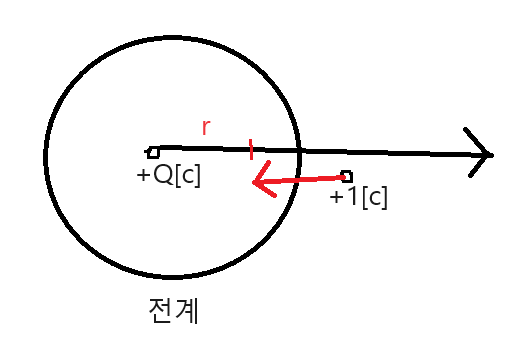
$V=-\int_{\infty}^{r}E.dr$
$V=\frac{Q}{4\pi\epsilon_{0}r}[V]$
●전위차

$V_a=\frac{Q}{4\pi\epsilon_{0}a}$
$V_b=\frac{Q}{4\pi\epsilon_{0}b}$
${\color{Red}V_{ab}=V_{a}-V_{b}=\frac{Q}{4\pi\epsilon_{0}}(\frac{1}{a}-\frac{1}{b})}$
●정전력 $F=\frac{1}{4\pi\epsilon_0}\times\frac{Q_{1}Q_{2}}{r^2}[N]$
↕ $F=Q.E\,\,\,\,\,\,\,E=\frac{F}{Q}$
전계의 세기 $E=\frac{1}{4\pi\epsilon_0}\times\frac{Q}{r^2}[V/m]$
↕ $E=-\triangledown.V\,\,\,\,\,\,\, V=-\int{E}.dr$
전위$V=\frac{Q}{4\pi\epsilon_{0}r}[V]$
*스칼라 기울기의 회전=0
$\triangledown\times{E}=0\,\,\,\,\triangledown\times(-\triangledown{V})=0$
비회전계(보존계)
$\int_{a}^{b}E.dl$=일정(경로와 무관하다.)
$\oint{E}.dl=\int\triangledown\times{E}ds=0$
● 등전위면
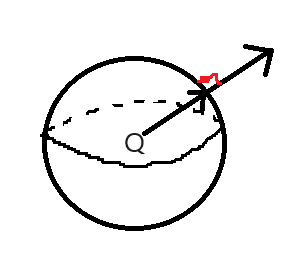
①등전위면은 폐곡면이다.
②서로 다른 등전위면은 교차하지 않는다.
③전기력선은 등전위면과 수직이다.
④점전하에 의한 등전위면은 구면이다.
●도체의 성질
*도체 : 자유 전하가 무수히 많은 물질.
← + +→
+→ ← -
①도체 내부에는 전하가 없다. → 도체 표면에 존재.
$E=\frac{Q}{4\pi\epsilon_{0}r^2}\to E=0$
②$E=-\triangledown{V}=0$
변화가 없다.
도체 내부=외부=표면 전위가 같다.
③전기력선은 도체 표면에 수직으로 출입한다,
④전하밀도는 곡률이 클수록 높다.
※ 곡률이 클수록=뽀족하다=곡률반경이 작을 수록
'전기(산업)기사필기 > 전기자기학' 카테고리의 다른 글
| 전기력선,전기력서의 특징,전기력선의 방정식,가우스법칙,포아송방정식,전속,전속밀도,전기자기학(전기기사) (2) | 2023.12.20 |
|---|---|
| 기초수학,삼각함수,피타고라스정리,미분적분,전기자기학(전기기사) (2) | 2023.12.03 |
| 원자의 구조,전하량,전기자기학(전기기사) (0) | 2023.12.01 |
| 벡터의 연산,더하기,빼기,내적,외적,기울기,발산,회전,전기자기학(전기기사) (0) | 2023.11.10 |
| 벡터와스칼라,성분벡터(기본벡터),단위벡터,직교좌표,직각좌표,원통좌표,구형좌표,전기자기학(전기기사) (0) | 2023.11.07 |



